Sistem Bilangan

	Pada dasarnya, komputer baru bisa bekerja kalau ada aliran listrik yang mengalir didalamnya. Dalam hal ini, aliran listrik yang mengalir ternyata memiliki dua kondisi, yaitu kondisi ON yang berarti ada arus listrik, dan kondisi OFF yang berarti tidak ada arus listrik. Berdasar hal tersebut kemudian dibuat perjanjian, bahwa kondisi ON diberi lambang 1 (angka satu), dan kondisi OFF diberi lambang 0 (angka nol).
	Seluruh data yang berupa angka, abjad ataupun special character kemudian ditulis dalam rangkaian kombinasi 0 dan 1, misal angka 5 ditulis dalam bentuk 000101 dan huruf D ditulis dalam 110100. Pabrik komputer membuat seluruh terjemahan ini dalam bentuk rangkaian elektronik yang tersimpan didalamnya.
	Dengan demikian, seandainya kita kemudian memasukkan tulisan yang berbunyi: I LOVE YOU melalui keyboard, tulisan ini secara otomatis akan diterjemahakan kedalam bentuk 1 dan 0 oleh komputer.
	Agar bisa dibaca oleh manusia, hasil terjemahan ini kemudian diterjemahkan kembali kedalam bentuk dan huruf ataupun angka seperti asalnya, dan kemudian dikeluarkan melalui layar monitor.
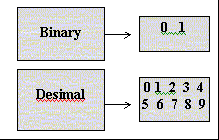
	Karena hanya memiliki 2 angka dasar, yaitu 0 dan 1, maka sistem bilangan semacam ini kemudian dikenal sebagai sistem bilangan biner (binary number). Untuk perbandingan, sistem bilangan yang telah kita kenal disebut sebagai sistem bilangan desimal; Disebut desimal karena memiliki angka dasar yang berjumlah 10, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9.
...no image yet...	a. Sistem Bilangan Desimal Sistem bilangan yang selama ini kita kenal adalah sistem bilangan desimal, dimana sistem bilangan desimal ini memiliki angka dari 0 hingga 9, dengan jumlah bilangan mencapai 10 buah. Dalam contoh terlihat, bahwa angka 3675 bisa diartikan sebagai (5X101) + (7X101) + (6X102) + (3X103). Angka 10 merupakan jumlah angka dasar yang dimiliki oleh bilangan desimal.
	b. Sistem Bilangan Binary Karena sistem bilangan binary hanya memiliki angka 0 dan 1 saja, maka nilai 11010 dalam bilangan biner dapat diartikan sebagai: (0X20) + (1X21) + (0X22) + (1X23) + (1X24) = 26. Angka 2 merupakan jumlah angka dasar yang dimiliki oleh bilangan biner
...no image yet...	Untuk mengkonversikan bilangan desimal ke-binary, maka langkah yang bisa dilakukan adalah : a. Apabila bilangan tersebut bisa dibagi dengan 2, maka hasilnya ditulis 0 pada sisi sebelah kanan (lihat gambar disebelah).Tetapi apabila tidak, maka angka 1 yang ditulis.
	Untuk melakukan penambahan pada bilangan binary, langkah yang dilakukan adalah sama dengan langkah penambahan pada bilangan desimal. Karena angka tertinggi yang dimiliki hanyalah angka 1, maka seandainya pada penjumlahan tersebut mehasilkan angka 2, maka akan ditulis 0 dengan catatan masih menyimpan 1. Seandainya pada penjumlahan menghasilkan angka 3, maka akan ditulis 1 dan masih menyimpan 1 (lihat contoh).
...no image yet...	Apabila dalam melakukan pengurangan ternyata angka yang dimiliki masih kurang nilainya, maka bisa diambil langkah dengan cara meminjam angka yang berada disebelah kiri. 1 angka apabila dipinjam/dipindah keposisi kanan, akan mempunyai nilai 2 (lihat contoh).
	Langkah yang dilakukan pada saat perkalian pada bilangan binary juga sama dengan langkah yang dilakukan pada bilangan desimal. Hal ini bisa dilihat pada contoh yang ada.
...no image yet...	Prinsip pembagian pada bilangan binary juga tidak berbeda dengan prinsip pembagian pada bilangan desimal. Hal ni bisa terlihat pada contoh yang ada.
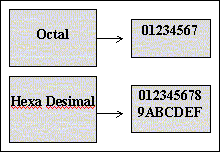
	c. Sistem Bilangan Octal dan Hexadesimal Selain menggunakan sistem binary, komputer juga menggunakan sistem bilangan octal, dimana mempunyai jumlah bilangan dasar sebanyak 8 dan sistem bilangan hexa-desimal yang mempunyai bilangan dasar sejumlah 16. Susunan angka yang dimiliki kedua bilangan, seperti yang nampak pada gambar.
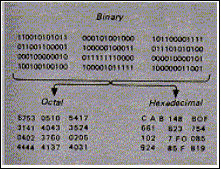
	Walaupun demikian, komputer tetap bekerja dengan menggunakan sistem binary. Angka dasar 8 dan 16 hanya dibutuhkan saat mengubah dari atau menjadi binary, dan dengan cara ini memungkin penulisan menjadi lebih ringkas dari nilai sebenarnya yang ada didalam memory komputer. Octal senantiasa ditulis dalam tiga angka dan hexa desimal dalam empat angka.
	Sistem bilangan Octal memiliki angka sebanyak 8 buah, yaitu dari angka 0 hingga 7. Untuk membuat konversi bilangan dari Oktal ke-desimal, digunakan angka dasar 8, karena sesuai dengan jumlah angka yang dimilikinya.
...no image yet...	Karena jumlah angka yang dimiliki oleh bilangan ini jumlahnya 16, maka angka 16 inilah yang dijadikan dasar untuk konversi ataupun perhitungan-perhitungan lainnya.
	d. System BCD Pada awalnya, system BCD (Binary Coded Decimal), menggunakan 4-bit guna menyajikan bilangan desimal. Setiap digit didalam bilangan desimal, akan dirubah kedalam bentuk 4-bit binary. sebagai contoh, bilangan 3752 didalam bilangan desimal, akan diubah menjadi 0011 0111 0101 0010.
	Karena dianggap tidak efisien, yaitu hanya sanggup menampung data sebanyak 24 atau 16 karakter yang berbeda, maka sistem BCD ini kemudian disempurnakan dengan menggunakan 6-bit guna menyajikan data yang ada. Dengan demikian, data yang disajikan akan menjadi lebih banyak lagi, yaitu 26 atau sejumlah 64 karakter yang berbeda-beda.
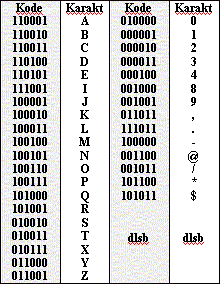
	f. System EBCDIC EBCDIC (Extended Binary Coded Decimal Interchange Code) menggunakan 8-bit guna menyajikan data yang ada. Dengan adanya 8-bit ini, tentu saja jumlah data yang disajikan menjadi lebih besar, yaitu sebanyak 28 atau 256 kombinasi. 4 karakter yang berada disebelah kiri disebut sebagai zone-bits, dan 4 karakter sisanya disebut sebagai numerik bits. Kode-kode ini banyak digunakan oleh komputer IBM ataupun peralatan yang menggunakan standart IBM. g. System ASCII ASCII (American Standart Code for Informa tion Interchange), menggunakan 7-bit guna menyajikan beberapa data. Sistem ini digunakan oleh beberapa pabrik komputer secara bersama-sama sehingga menghasilkan suatu standart yang baku untuk semua jenis komputer. Walaupun ASCII menggunakan kode 7-bit , tetapi dalam pelaksanaannya tetaplah 8-bit yang digunakan. Sebab masih menggunakan extra bit yang digun